贪心算法是一种在每一步选择中都采取当前状态下最优（即最有利）的选择，从而希望导致结果是全局最优的算法策略。

参考文章：

贪心算法（Greedy Algorithm）

【算法/训练】：贪心（算法理论学习及实践）

＜贪心算法＞学习及经典实例分析

贪心算法详解

基本定义

贪心算法（Greedy Algorithm）是一种分阶段决策策略：在对问题求解时，总是做出在当前看来是最好的选择的算法，也就是当前状态的局部最优解，通过迭代累积这些局部最优解，期望得到全局最优解。其核心特征是 “无后效性”（当前决策不影响后续状态）和 “贪心选择性质”（局部最优可推导全局最优）。贪心算法的核心在于贪心策略的选择，即每一步的最优选择是否能推导出全局最优解。

贪心算法的价值在于其简洁性与高效性，但必须警惕其局限性——局部最优未必全局最优。掌握其适用条件（贪心选择性质+最优子结构）和证明方法，方能灵活应用于任务调度、图论、组合优化等场景。

核心性质

贪心算法采用自顶向下，以迭代的方法做出相继的贪心选择，每做一次贪心选择就将所求问题简化为一个规模更小的子问题，通过每一步贪心选择，可得到问题的一个最优解，虽然每一步上都要保证能获得局部最优解，但由此产生的全局解有时不一定是最优的，所以贪婪法不要回溯。能够用贪心算法求解的问题一般具有两个重要特性：贪心选择性质和最优子结构性质

贪心选择性质：每一步的最优解不依赖于未来决策或子问题的解。
- 所求问题的整体最优解可以通过一系列局部最优的选择，即贪心选择来达到。这是贪心算法可行的第一个基本要素。
- 对于一个具体问题，要确定它是否具有贪心选择性质，必须证明每一步所作的贪心选择最终导致问题的整体最优解。
- 证明的大致过程如下：
  - 首先考察问题的一个整体最优解，并证明可修改这个最优解，使其以贪心选择开始。
  - 做了贪心选择后，原问题简化为规模更小的类似子问题。
  - 然后用数学归纳法证明通过每一步做贪心选择，最终可得到问题的整体最优解。
  - 其中，证明贪心选择后的问题简化为规模更小的类似子问题的关键在于利用该问题的最优子结构性质
最优子结构：问题的最优解包含其子问题的最优解，与动态规划共享此性质，但贪心算法无需回溯或存储子问题解。
无后效性：决策一旦做出，不可更改，后续状态仅由当前状态决定。

贪心算法与动态规划的差异

动态规划和贪心算法都是一种递推算法，均有最优子结构性质，通过局部最优解来推导全局最优解。
两者之间的区别在于：
- 贪心算法中作出的每步贪心决策都无法改变，因为贪心策略是由上一步的最优解推导下一步的最优解，而上一步之前的最优解则不作保留，贪心算法每一步的最优解一定包含上一步的最优解。
- 动态规划算法中全局最优解中一定包含某个局部最优解，但不一定包含前一个局部最优解，因此需要记录之前的所有最优解。

算法框架

贪心算法的通用实现步骤：

定义问题目标与约束条件

设计贪心选择策略（如排序、优先队列）

迭代选择局部最优解

验证并合并解到全局解

终止条件：问题规模归零或约束满足

算法思路：

建立数学模型来描述问题；
把求解的问题分成若干个子问题；
对每个子问题进行求解，得到子问题的局部最优解；
把子问题的解（局部最优解）合成原来问题的解；

算法实现：

从问题的某个初始解出发；
采用循环语句，当可以向求解目标前进一步时，就根据局部最优策略，得到一个部分解，缩小问题的范围或规模；
将所有部分解综合起来，得到问题的最终解；

使用情况

举个例子： 有 6 张纸币，面额分别为 100，70，50， 20，20，10，现在我们可以拿走 3 张纸币，要求总金额最大，该怎么拿

一看到这个问题，肯定就会想着拿最大的那三张就行了，其实这个想法是没错的，但可以把这个想法分解一下：
不考虑拿 3 张，只考虑拿走一张的最大值（局部最优），那这个问题就可以拆解为拿三次的情况，第一次拿 100，第二次拿 70，第三次拿 50，那我们最多可以拿 220

典型应用场景

任务调度与区间问题
- 活动选择：最大化不重叠活动数量（按结束时间排序）。
- 会议室安排：最小化会议室使用数量（转化为区间重叠计数）。
图论问题
- 最小生成树
  - Prim算法：从单点出发，每次选择与树相连的最小边。
  - Kruskal算法：按边权升序排序，选择不形成环的边。
- 最短路径
  - Dijkstra算法：从源点出发，每次选择距离最小的未处理节点。
组合优化问题
- 分数背包：按单位价值排序，优先装入高价值物品。
- 找零问题：硬币面额满足贪心性质时（如人民币面额），优先使用大面额硬币。

经典例题详解

最小合并代价
问题：合并n个部落，每次合并代价为两部落人数之和，求最小总代价。
解法：优先队列（最小堆）每次合并最小的两个数。

import heapq
def min_cost(nums):
    heapq.heapify(nums)
    cost = 0
    while len(nums) > 1:
        a = heapq.heappop(nums)
        b = heapq.heappop(nums)
        cost += a + b
        heapq.heappush(nums, a + b)
    return cost

纪念品分组
问题：将物品两两分组，每组和不超过W，求最少组数。
解法：排序后双指针配对（最大与最小配对）。

def min_groups(items, W):
    items.sort()
    left, right = 0, len(items) - 1
    groups = 0
    while left <= right:
        if items[left] + items[right] <= W:
            left += 1
        right -= 1
        groups += 1
    return groups

变种与挑战问题
1. 加油站问题
  - 环形路线上，每个加油站有油量gas[i]，从第i站到下一站耗油cost[i]，求可行起点。
  - 贪心策略：若当前剩余油量<0，则起点设为下一站，重置油量。
2. 数列极差问题
  - 操作：每次擦去两数a、b，加入a×b+1，求最终数的极差（max-min）。
  - 解法：最小化时合并最大数，最大化时合并最小数。
实战训练建议
- 入门题库：LeetCode “Assign Cookies”（分配问题）、”Best Time to Buy and Sell Stock II”（股票买卖）。
- 进阶挑战：蓝桥杯 “答疑”（按s+a升序排序减少等待时间）、HackerRank “Greedy Florist”。
- 竞赛考点：贪心常与排序、堆、双指针结合，需重点训练边界条件处理。

贪心策略的代码实现范式

关键数据结构

优先队列（堆）：用于快速获取最小值/最大值（如合并果子问题）。
排序预处理：为贪心选择创造条件（如区间调度需按结束时间排序）。

经典问题实现

区间调度（最大不重叠区间）

问题描述：从一组区间中选择最多数量的互不重叠区间。
贪心策略：按结束时间升序排序，优先选择结束早的区间。
时间复杂度：O(n log n)，主要来自排序操作。

def max_non_overlapping(intervals):
    intervals.sort(key=lambda x: x[1])  # 按结束时间排序
    count = 0
    last_end = -float('inf')
    for start, end in intervals:
        if start >= last_end:
            count += 1
            last_end = end
    return count

哈夫曼编码（数据压缩）

问题描述：构造字符的最优前缀编码树，使带权路径长度最小。
贪心策略：每次合并频率最小的两个节点。

import heapq
def build_huffman_tree(data):
    freq = {}
    for char in data:
        freq[char] = freq.get(char, 0) + 1
    heap = [[weight, [char, ""]] for char, weight in freq.items()]
    heapq.heapify(heap)
    while len(heap) > 1:
        lo = heapq.heappop(heap)
        hi = heapq.heappop(heap)
        for pair in lo[1:]:
            pair[1] = '0' + pair[1]
        for pair in hi[1:]:
            pair[1] = '1' + pair[1]
        heapq.heappush(heap, [lo[0] + hi[0]] + lo[1:] + hi[1:])
    return heap[0]

正确性证明与复杂度分析

证明方法

数学归纳法：证明每一步贪心选择均保持最优子结构。
反证法：假设存在更优解，通过替换操作证明贪心解更优（如区间调度问题）。
构造法：展示贪心解可逐步扩展为全局最优解（如哈夫曼树构造）。

复杂度分析

问题类型	时间复杂度	空间复杂度
区间调度	O(n log n)	O(1)
哈夫曼编码	O(n log n)	O(n)
最小生成树（Prim）	O(E log V)	O(V)

适用条件判断

贪心算法仅适用于满足以下性质的问题：

贪心选择性质：局部最优可推导全局最优。
最优子结构：子问题最优解可组合为原问题最优解。
不适用场景：当前选择影响未来状态（如0-1背包问题需用动态规划）。

算法题

分发糖果

题目链接：LeetCode_135. 分发糖果

问题描述：
n 个孩子站成一排。给你一个整数数组 ratings 表示每个孩子的评分。需要按照以下要求，给这些孩子分发糖果：
每个孩子至少分配到 1 个糖果；相邻两个孩子中，评分更高的那个会获得更多的糖果。
请你给每个孩子分发糖果，计算并返回需要准备的 最少糖果数目 。

示例 1：
输入：ratings = [1,0,2]
输出：5
解释：你可以分别给第一个、第二个、第三个孩子分发 2、1、2 颗糖果。

示例 2：
输入：ratings = [1,2,2]
输出：4
解释：可以分别给第一个、第二个、第三个孩子分发 1、2、1 颗糖果。第三个孩子只得到 1 颗糖果，这满足题面中的两个条件。

提示：
n == ratings.length
1 <= n <= 2 * 10^4
0 <= ratings[i] <= 2 * 10^4

public int candy(int[] ratings) {
    int[] candyVec = new int[ratings.length]; // 每个小孩分的糖果
    Arrays.fill(candyVec, 1);
    // 从左往右遍历
    for(int i = 1; i < ratings.length; i++){
        if(ratings[i] > ratings[i - 1]){
            candyVec[i] = candyVec[i - 1] + 1;
        }
    }
    // 从右往左遍历
    for (int i = ratings.length - 2; i >= 0; i--) {
        if (ratings[i] > ratings[i + 1] ) {
            candyVec[i] = Math.max(candyVec[i], candyVec[i + 1] + 1);
        }
    }
    // 统计结果
    int result = 0;
    for (int i = 0; i < candyVec.length; i++) {
        result += candyVec[i];
    }
    return result;
}

盛最多水的容器

题目链接：LeetCode_11. 盛最多水的容器

问题描述：
给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。返回容器可以储存的最大水量。
说明：你不能倾斜容器。

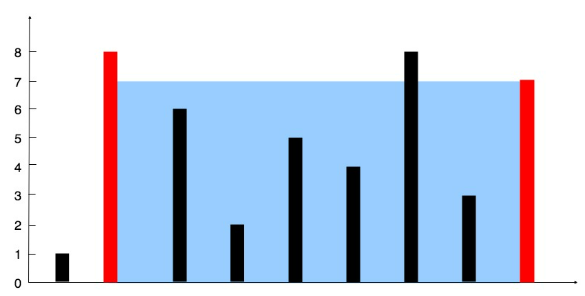
示例 1：
输入：[1,8,6,2,5,4,8,3,7]
输出：49
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：
输入：height = [1,1]
输出：1

提示：
n == height.length
2 <= n <= 10^5
0 <= height[i] <= 10^4

public int maxArea(int[] height) {
   int r = height.length - 1, max = 0;
   for (int l = 0; l < r; ) {
       max = Math.max(max, Math.min(height[l], height[r]) * (r - l));
       if (height[l] < height[r]) {
            l++;
       } else {
           r--;
       }
   }
   return max;
}

背包问题

问题描述：
有一个背包，背包容量是M=150。有7个物品，物品可以分割成任意大小。要求尽可能让装入背包中的物品总价值最大，但不能超过总容量。
物品：A B C D E F G
重量：35 30 60 50 40 10 25
价值：10 40 30 50 35 40 30

问题分析：

目标函数：∑pi 求和，最大，使得装入背包中的所有物品 pi 的价值加起来最大；

约束条件：装入的物品总重量不超过背包容量：∑wi <= M( M=150)；

贪心策略：

选择价值最大的物品。

选择重量最小的物品。

选择单位重量价值最大的物品。

1、值得注意的是，贪心算法并不是完全不可以使用，贪心策略一旦经过证明成立后，它就是一种高效的算法。
2、贪心算法还是很常见的算法之一，这是由于它简单易行，构造贪心策略不是很困难。
3、可惜的是，它需要证明后才能真正运用到题目的算法中。

一般来说，贪心算法的证明围绕着：整个问题的最优解一定由在贪心策略中存在的子问题的最优解得来的。对于背包问题中的 3 种贪心策略，都是 无法成立（无法被证明） 的，解释如下：

选取价值最大者：W=30

物品重量价值

A 28 30

B 12 20

C 12 20

根据策略，首先选取物品A，接下来就无法再选取了，可是，选取B和C一起，则更好。
选取重量最小者：选取重量最小。它的反例与第一种策略的反例差不多。
选取单位重量价值最大者：W=30

物品重量价值

A 28 28

B 20 20

C 10 10

物品	重量	价值
A	28	30
B	12	20
C	12	20

物品	重量	价值
A	28	28
B	20	20
C	10	10

根据策略，三种物品单位重量价值一样，程序无法依据现有策略作出判断，如果选择A，则答案错误。但是如果在条件中加一句当遇见单位价值相同的时候，优先装重量小的，这样的问题就可以解决。

以下这个算法里面就是采用的贪心第三方案，一般这个方案是成功率最大的。

public static void main(String[] args) {
    Scanner scanner = new Scanner(System.in);
    int n = scanner.nextInt(); // n：物品个数
    int m = scanner.nextInt(); // m：背包容量
    List<Package> p = new ArrayList<>();
    for (int i = 0; i < n; i++) { // 输入物品的重量和价值
        int weight = scanner.nextInt();
        int value = scanner.nextInt();
        double average = value / weight * 1.0;
        p.add(new Package(weight, value, average));
    }
    // 排序默认升序，需要自定义为降序
    Collections.sort(p, (pac1, pac2) -> Double.compare(pac2.avg, pac1.avg));
    int maxValue = 0;
    for (int i = 0; i < n; i++) {
        if (m >= p.get(i).weight) {
            m -= p.get(i).weight;
            maxValue = maxValue + p.get(i).value;
        } else {
            break;
        }
    }
    System.out.println(maxValue);
}
public static class Package {
    public int weight;         // 重量
    public int value;          // 价值
    public double avg;         // 单位价值
    public Package(int weight, int value, double avg) {
        this.weight=weight;
        this.value=value;
        this.avg=avg;
    }
}

购物清单（带条件的背包问题）

题目链接：牛客网_HJ16 购物单

问题描述：王强决定把年终奖用于购物，他把想买的物品分为两类：主件与附件。

主件可以没有附件，至多有 22 个附件。附件不再有从属于自己的附件。

若要购买某附件，必须先购买该附件所属的主件，且每件物品只能购买一次。

王强查到了 m 件物品的价格，而他只有 n 元的预算。为了先购买重要的物品，他给每件物品规定了一个重要度，用整数 1∼5 表示。他希望在不超过预算的前提下，使满意度最大。满意度定义为所购每件物品价格与重要度乘积之和。

输入描述：第一行输入两个整数 n,m代表预算、查询到的物品总数。
此后 m 行，第 i 行输入三个整数 vi, wi, qi 分别代表价格、重要度、主件编号。特别地， qi = 0,代表该物品为主件，否则表示该附件从属于主件。编号即输入顺序，从1开始。保证全部物品的价格 v 均为 10 的倍数；且每个主件的附件数不超过 2 个。

输出描述：在一行上输出一个整数，代表王强可获得的最大满意度。
1
2
3
4
5
6
7
8
9
10
输入
50 5
20 3 5
20 3 5
10 3 0
10 2 0
10 1 0
输出 130
说明：在这个样例中，第三、四、五件物品为主件，第一、二件物品为第五件物品的附件。这就意味着，如果购买了第一件物品或第二件物品，则必须购买第五件物品；但是特别地，如果同时购买了第一件物品和第二件物品，则只需要购买一次第五件物品。
我们可以证明，购买一、二、五件商品，获得的满意度最大，为 20×3+20×3+10×1=130。

public static void main(String[] args) {
    Scanner in = new Scanner(System.in);
    int n = in.nextInt(); // 预算
    int m = in.nextInt(); // 物品数
    if(n <= 0 || m <= 0) System.out.println(0);
    Package[] p = new Package[m + 1];
    int[][] appendix =  new int[m + 1][2]; // 附件 最多2个
    for (int i = 1; i <= m; i++) { // 输入物品 价格、重要度、主件编号
        int vi = in.nextInt(); // weight
        int wi = in.nextInt(); // value
        int qi = in.nextInt();
        p[i] = new Package(vi, wi, qi);
        if (qi > 0) {
            if (appendix[qi][0] == 0) {
                appendix[qi][0] = i;
            } else {
                appendix[qi][1] = i;
            }
        }
    }
    int[][] dp = new int[m + 1][n + 1]; // 动态规划
    for (int i = 1; i <= m; i++) {
        Package item = p[i];
        int vi = p[i].vi;
        int dp0 = p[i].wi * vi; // 只有主件
        int dp1 = 0, dp2 = 0, dp3 = 0, v1 = 0, v2 = 0, v3 = 0;
        if (appendix[i][0] != 0) { // 附件1
            v1 = vi + p[appendix[i][0]].vi;
            dp1 = dp0 + p[appendix[i][0]].wi * p[appendix[i][0]].vi;
        }
        if (appendix[i][1] != 0) { // 附件2
            v2 = vi + p[appendix[i][1]].vi;
            dp2 = dp0 + p[appendix[i][1]].wi * p[appendix[i][1]].vi;
        }
        if (appendix[i][0] != 0 && appendix[i][1] != 0) { // 附件1, 2
            v3 = vi + p[appendix[i][0]].vi + p[appendix[i][1]].vi;
            dp3 = dp0 + p[appendix[i][0]].wi * p[appendix[i][0]].vi + 
                p[appendix[i][1]].wi * p[appendix[i][1]].vi;
        }
        for (int j = 1; j <= n; j++) {
            dp[i][j] = dp[i - 1][j];
            if (p[i].qi == 0) { // 主件
                if(j >= vi && vi != 0) dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - vi] + dp0);
                if(j >= v1 && v1 != 0) dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - v1] + dp1);
                if(j >= v2 && v2 != 0) dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - v2] + dp2);
                if(j >= v3 && v3 != 0) dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - v3] + dp3);
            }
        }
    }
    System.out.println(dp[m][n]);
}
public static class Package {
    public int vi;         // 价格
    public int wi;          // 重要性
    public int qi;      // 0 为主件 否则为为从属主件parent - 1
    public Package(int vi, int wi, int qi) {
        this.vi=vi;
        this.wi=wi;
        this.qi=qi;
    }
}

活动时间安排问题

问题描述：

设有 n个活动的集合 E={1,2,…,n}，其中每个活动都要求使用同一资源，如：演讲会场等，而在同一时间内只有一个活动能使用这一资源。每个活动 i 都有一个要求使用该资源的起始时间 si 和一个结束时间 fi ,且 si < fi 。要求设计程序，使得安排的活动最多。
注：活动结束时间从小到大排序

i	1	2	3	4	5	6	7	8	9	10	11
S[i]	1	3	0	5	3	5	6	8	8	2	12
f[i]	4	5	6	7	8	9	10	11	12	13	14

问题分析：

活动安排问题要求安排一系列争用某一公共资源的活动。贪心算法可提供一个简单、漂亮的方法，使尽可能多的活动能兼容的使用公共资源。设有 n 个活动的集合｛0，1，2，…，n-1｝，其中每个活动都要求使用同一资源，如会场等，而在同一时间内只有一个活动能使用这一资源。每个活动 i 都有一个要求使用该资源的起始时间 starti 和一个结束时间 endi ，且 starti < endi。如选择了活动 i，则它在半开时间区间 [starti, endi) 内占用资源。若区间 [starti,endi) 与区间 [startj,endj) 不相交，称活动 i 与活动 j 是相容的。即，当 startj ≥ endi 或 starti ≥ endj 时，活动 i 与活动 j 相容。活动安排问题就是在所给的活动集合中选出最多的不相容活动。

算法设计：

若被检查的 活动 i 的开始时间 starti 小于最近选择的 活动 j 的结束时间 endj，则不选择 活动 i，否则选择 活动 i 加入集合中。运用该算法解决活动安排问题的效率极高。当输入的活动已按结束时间的非减序排列，算法只需 O(n) 的时间安排 n 个活动，使最多的活动能相容地使用公共资源。如果所给出的活动未按非减序排列，可以用 O(nlogn) 的时间重排。

代码实现一：

public static void main(String[] args) {
    Scanner scanner = new Scanner(System.in);
    int n = scanner.nextInt();     // n：活动个数
    List<Active> act = new ArrayList<>();
    for (int i = 0; i < n; i++) {  // 输入开始和结束
        int start = scanner.nextInt();
        int finish = scanner.nextInt();
        act.add(new Active(start, finish));
    }
    // 将活动按活动结束时间从小到大排序
    Collections.sort(act, (o1, o2) -> o1.finish - o2.finish);
    int t = -1; // t：与各个活动的起始时间相比较
    int total = 0; // total：最后的活动的个数
    for (int i = 0; i < n; i++) { //循环访问所有活动
        if (t <= act.get(i).start) {
            total ++;
            t = act.get(i).finish;
        }
    }
    System.out.println(total);
}
public static class Active {
    public int start;     // 开始时间
    public int finish;    // 结束时间
    public Active(int start, int finish) {
        this.start=start;
        this.finish=finish;
    }
}

代码实现二：

public static void main(String[] args) {
    int N = 11; // 活动数
    // 将活动时间进行静态数组直接存储
    int[] s = {0, 1, 3, 0, 5, 3, 5, 6, 8, 8, 2, 12}; // 下标从1开始,存储活动开始时间
    int[] f = {0, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14}; //下标从1开始,存储活动结束时间
    boolean[] A = new boolean[N + 1];
    System.out.println("各活动的开始时间,结束时间分别为：");
    for (int i = 1; i <= N; i++) {
        System.out.println("[" + i + "]:" + "(" + s[i] + "," + f[i] + ")");
    }
    GreedySelector(N, s, f, A);
    for (int i = 1; i < N; i++) {
        if (A[i]) {
            System.out.println("[" + i + "]:" + "(" + s[i] + "," + f[i] + ")");
        }
    }
}
private static void GreedySelector(int n, int[] s, int[] f, boolean[] A) {
    A[1] = true;
    int j = 1; // 记录最近一次加入A中的活动
    for (int i = 2; i <= n; i++){ // 依次检查活动i是否与当前已选择的活动相容
        if (s[i] >= f[j]) {
            A[i] = true;
            j = i;
        } else {
            A[i] = false;
        }
    }
}

注意：虽然贪心算法不是一定可以得到最好的解，但是对于这种活动时间的问题，他却得到的总是最优解，这点可用数学归纳法证明。在这里，体现出来的贪心策略是：每一个活动时间的挑选总是选择最优的，就是刚好匹配的，这样得出的结果也就是最优的了。

最小生成树（克鲁斯卡尔算法）

在连通网中查找最小生成树的常用方法有两个，分别称为普里姆（Prim）算法和克鲁斯卡尔（Kruskal）算法。

克鲁斯卡尔算法 查找最小生成树的方法是：将连通网中所有的边按照权值大小做升序排序，从权值最小的边开始选择，只要此边不和已选择的边一起构成环路，就可以选择它组成最小生成树。对于 N 个顶点的连通网，挑选出 N-1 条符合条件的边，这些边组成的生成树就是最小生成树。

问题描述：求一个连通无向图的最小生成树的代价（图边权值为正整数）。

输入：第一行是一个整数N（1<=N<=20），表示有多少个图需要计算。以下有N个图，第i图的第一行是一个整数M（1<=M<=50），表示图的顶点数，第i图的第2行至1+M行为一个M*M的二维矩阵，其元素ai,j表示图的i顶点和j顶点的连接情况，如果ai,j=0，表示i顶点和j顶点不相连；如果ai,j>0，表示i顶点和j顶点的连接权值。

输出：每个用例，用一行输出对应图的最小生成树的代价。

样例输入：

1
6
0 6 1 5 0 0
6 0 5 0 3 0
1 5 0 5 6 4
5 0 5 0 0 2
0 3 6 0 0 6
0 0 4 2 6 0

样例输出：15

问题分析：

边的选择要求从小到大选择，则开始显然要对边进行升序排序；
选择的边是否需要，则从判断该边加入后是否构成环；

算法设计：

对边进行升序排序：在此采用链式结构，通过插入排序完成。每一结点存放一条边的左右端点序号、权值及后继结点指针；
边的加入后，是否会构成环：最开始假定各顶点分别为一组，其组号为端点序号。选择某边后看其两端点是否在同一组中，即所在组号是否相同，若是，表示构成了环，则舍去。若两个端点所在的组不同，则表示可以加入，则将该边两端的组合并成同一组。

代码实现：

public static void main(String[] args) {
    Scanner scanner = new Scanner(System.in);
    int V = scanner.nextInt(); // V是顶点数
    int E = scanner.nextInt(); // E是边数
    Edge[] edge = new Edge[E]; // 存储边的数组
    for (int i = 0; i < E; ++i) {
        edge[i] = new Edge();
    }
    kruskal(V, edge);
}
// 执行克鲁斯卡尔算法
public static void kruskal(int V, Edge[] edge) {
    Edge result[] = new Edge[V]; // 存储结果的数组
    int e = 0; // 表示result数组中的下标
    Arrays.sort(edge);  // 将边按照权重从小到大排序
    Subset subsets[] = new Subset[V]; // 创建V个子集
    for (int i = 0; i < V; ++i) { // 初始化每个子集的父节点和秩
        subsets[i] = new Subset(i, 0);
    }
    // 取E-1条边
    int i = 0;
    while (e < V - 1) {
        Edge next_edge = edge[i++];
        int x = findParentNode(subsets, next_edge.src);
        int y = findParentNode(subsets, next_edge.dest);
        // 如果两个节点不在同一个集合中，合并它们
        if (x != y) {
            result[e++] = next_edge;
            unionSubsets(subsets, x, y);
        }
    }
    // 打印结果
    System.out.println("Following are the edges in the constructed MST");
    for (i = 0; i < e; ++i){
        System.out.println(result[i].src + " - " + result[i].dest + " - " + result[i].weight);
        return;
    }
}
// 查找父节点
public static int findParentNode(Subset subsets[], int i) {
    if (subsets[i].parent != i)
        subsets[i].parent = findParentNode(subsets, subsets[i].parent);
    return subsets[i].parent;
}
// 合并两个子集
public static void unionSubsets(Subset subsets[], int x, int y) {
    int xroot = findParentNode(subsets, x);
    int yroot = findParentNode(subsets, y);
    if (subsets[xroot].rank < subsets[yroot].rank){
        subsets[xroot].parent = yroot;
    } else if (subsets[xroot].rank > subsets[yroot].rank) {
        subsets[yroot].parent = xroot;
    } else {
        subsets[yroot].parent = xroot;
        subsets[xroot].rank++;
    }
}
// 定义边的数据结构
public static class Edge implements Comparable<Edge> {
    int src, dest, weight;
    public int compareTo(Edge edge) {
        return this.weight - edge.weight;
    }
}
// 并查集数据结构
public static class Subset {
    int parent;
    int rank;
    Subset(int parent, int rank) {
        this.parent=parent;
        this.rank=rank;
    }
}
// --------------------------- 无用 --------------------------
// 定义一个辅助函数，用于查找结点所在的集合
private static int findNode(int parent[], int i) {
    if (parent[i] == -1)
        return i;
    return findNode(parent, parent[i]);
}
// 定义一个辅助函数，用于合并两个集合
private static void unionNode(int parent[], int x, int y) {
    int xset = findNode(parent, x);
    int yset = findNode(parent, y);
    parent[xset] = yset;
}

线段覆盖（Lines cover）

问题描述：在一维空间中告诉你N条线段的起始坐标与终止坐标，要求求出这些线段一共覆盖了多大的长度。

解题思路：上述的表格中的数据代表10条线段的起始点和终点，对他们的起始点从小到大按顺序排列。

public static void main(String[] args) {
    int[] start = {2,3,4,5,6,7,8,9,10,11};  // 起始点
    int[] end = {3,5,7,6,9,8,12,10,13,15}; // 终点
    int total_len = 1;  //至少的长度为：3-2
    for (int i = 1, j = 0; i < 10; i++) {
        if (start[i] >= end[j]) { // 不相交
            total_len = total_len + end[i] - start[i];
            j = i;
        } else {
            if (end[i] <= end[j]) { // 重叠
                continue;
            } else { // 相交
                total_len = total_len + end[i] - end[j];
                j = i;
            }
        }
    }
    System.out.println(total_len);
}

数字组合问题

问题描述：设有N个正整数，现在需要你设计一个程序，使他们连接在一起成为最大的数字。

输入：

1 2	3 12 456 342

输出：45634212

程序要求：输入整数N 接下来一行输入N个数字，最后一行输出最大的那个数字。

题目解析：

首先想到如何使两个数连接在一起最大，例如 12 和 456 ，连接在一起有两种情况分别为 12456 和 45612 ，显然后者比前者大。

如果是多个正整数连在一起，我们则需要对元素进行比较，很显然这是一个排序的过程，而且需要相邻的元素两两比较，由此可以想到 冒泡排序：

public static void main(String[] args) {
    // 利用冒泡排序来实现升序序列
    int[] arr = {4, 2, 8, 0, 5, 7, 1, 3, 9};
    // 开始冒泡排序 总共排序轮数为：元素个数 - 1
    for (int i = 0; i < arr.length - 1; i++) {
        // 内层对比循环 次数 = 元素个数 - 排序轮数 - 1
        for (int j = 0; j < arr.length - i - 1; j++) {
            // 如果第一个数字比第二个数字大，实现交换这两个数字
            if (arr[j] > arr[j + 1]) {
                int temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
        }
    }
}

若有四个数字：456、12、342、78
1、先进行比较 456 和 12，发现 45612 比 12456 更大，此时交换两个数字的位置：12、456、342、78
2、再进行比较 456 和 342，发现 456342 比 342456 更大，再次进行位置的交换：12、342、456、78
3、在进行比较 456 和 78，发现 78456 比 45678 更大，无需进行交换；
4、最后顺序：12 、342 、456 、78

分析到这其实发现要想连接到一起的数字最大，其实需要排序的是每个数字的第一位，最终每个数字的第一位排序得到： 1,3,4,7;

综上所述，解题思路：就是在相邻两个正整数连接起来比较大小的基础上再对所有数字冒泡排序，即可完成题目要求：

public static void main(String[] args) {
    Scanner scanner = new Scanner(System.in);
    int num = scanner.nextInt();
    int[] arr = new int[num];
    for (int i = 0; i < num; i++) {
        arr[i] = scanner.nextInt();
    }
    for (int i = 0; i < num; i++) {
        for (int j = 0; j < num - i - 1; j++) {
            //如果 arr[j] 大于 arr[j+1]，则交换，否则，不交换
            if(compare(arr[j], arr[j+1])) {
                 int temp = arr[j];
                 arr[j]   = arr[j+1];
                 arr[j+1] = temp;
               // Collections.swap(list, i, j); //交换
            }
        }
    }
    for (int i = num - 1; i >= 0; --i){
        System.out.print(arr[i]);
    }
}
// 自定义排序  num1：:12，num2：456
public static boolean compare(int num1, int num2) {
    int count1 = 0, count2 = 0;
    int nm1 = num1, nm2 = num2;
    while (nm1 > 0) {
        count1++;   //用来得到 num1 的位数：2
        nm1 /= 10;
    }
    while (nm2 > 0) {
        count2++;   //用来得到 num2 的位数：3
        nm2 /= 10;
    }
    // Math.pow(a, b)：求 a 的 b 次方，这里用作将两个数连接起来进行下一步的比较
    double a = num1 * Math.pow(10.0, count2) + num2; // 表示组合数：num1 num2：12  * 1000 + 456 = 12456
    double b = num2 * Math.pow(10.0, count1) + num1; // 表示组合数：num2 num1：456 * 100  + 12  = 45612
    return Double.compare(a, b) == 1 ? true : false; // true表示组合数(num1 num2)大于组合数(num2 num1)
}

拼数

题目链接：牛客网_拼数

描述：设有n个正整数（n ≤ 20），将它们联接成一排，组成一个最大的多位整数。例如：n=3时，3个整数13，312，343联接成的最大整数为：34331213。又如：n=4时，4个整数7，13，4，246联接成的最大整数为：7424613
输入描述：第一行，一个正整数n。第二行，n个正整数。
输出描述: 一个正整数，表示最大的整数

示例1
输入：
1
2
3
13 312 343
输出：34331213

示例2
输入：
1
2
20
921650139 925571586 931563581 923960668 870548039 358493469 371229218 737101511 514654859 185379933 19421244 117259400 301947570 48520742 79303948 222979736 153546206 250582036 106394401 198125223
输出：
1
931563581925571586923960668921650139870548039793039487371015115146548594852074237122921835849346930194757025058203622297973619812522319421244185379933153546206117259400106394401
解析：

先把整数化成字符串，然后再比较a+b和b+a，如果a+b>b+a，就把a排在b的前面，反之则把a排在b的后面，最后输出排序后的字符串，即可得到最大的整数（如果求最小的整数，则从小到大排序）。

举例说明：a=‘123’，b=‘71’，a+b=’12371’，b+a=‘71123’，所以a+b<b+a，将b排在前面** 注意：正常的字符串存在比较缺陷，**如：A=’321’，B=’32’，按照标准的字符串比较规则因为A>B，所以A+B > B+A ，而实际上’32132’ < ’32321’。具体步骤如下：

获取n

依次获取n个正整数，将整数转换为字符串：声明字符串数组a[n]，将获取到的正整数存入数组a中，即可实现正整数到字符串的转换

自定义排序函数：若a+b > b+a，则把a排在前面，否则将b排在前面（对字符串a、b，a+b表示连接两个字符串形成一个新串）

从大到小输出排序后的字符串即可得到最大的整数

public static void main(String []args){
    Scanner sc = new Scanner(System.in);
    int n = sc.nextInt();
    sc.nextLine();
    String[] strArray = sc.nextLine().split(" "); // 
    // 自定义排序
    for(int k = 0; k < n; k++){
        for(int m = 0; m < n-1-k; m++){
            if(!sortStr(strArray[m], strArray[m + 1])){
                String temp = strArray[m];
                strArray[m] = strArray[m + 1];
                strArray[m + 1] = temp;
            }
        }
    }
    for(int i = 0; i<n;i++){
        System.out.print(strArray[i]);
    } 
}
// 排序函数实现
public static boolean sortStr(String str1,String str2){
    char[] char1 = (str1 + str2).toCharArray();
    char[] char2 = (str2 + str1).toCharArray();
    for(int i = 0; i < char1.length; i++){
        if(char1[i] > char2[i]) return true;
        else if(char1[i] < char2[i]) return false;
    }
    return false;
}

找零钱问题

在贪心算法里面最常见的莫过于找零钱的问题了。

问题描述：对于人民币的面值有1元、5元、10元、20元、50元、100元，下面要求设计一个程序，输入找零的钱，输出找钱方案中最少张数的方案，比如： 123元，最少是 1 张100 的，1 张 20 的，3 张 1 元的，一共5张。

问题解析：运用的贪心策略是每次选择最大的钱，如果最后超过了，再选择次大的面值，然后次次大的面值，一直到最后与找的钱相等。

代码实现：

public static void main(String[] args) {
    Scanner scanner = new Scanner(System.in);
    int money = scanner.nextInt();                  // money：需要的交换的钱数
    int[] moneyClass = {100,50,20,10,5,1};          // 记录钱的面值
    int[] moneyNum = new int[6];                    // 记录各种面值的数量
    int moneyCount = 0, count = 0;
    for (int i = 0; i <= moneyClass.length; i++) {
        if (moneyCount + moneyClass[i] > money) {   // 如果需要的钱数小于最大的面值
            i++;
            continue;                               // 换用更小的面值，继续去判断
        }
        moneyCount += moneyClass[i];
        moneyNum[i] ++;
        count ++;
        while (moneyCount == money) {
            break;
        }
    }
    System.out.println("一共需要：" + count + "张纸钱。" );
    // 输出张数
    for (int i = 0; i < 6; i++) {
        if (moneyNum[i] != 0) {
            switch (i) {
                case 0: System.out.println("面值为100的有：" + moneyNum[i] + "张"); break;
                case 1: System.out.println("面值为50的有：" + moneyNum[i] + "张"); break;
                case 2: System.out.println("面值为20的有：" + moneyNum[i] + "张"); break;
                case 3: System.out.println("面值为10的有：" + moneyNum[i] + "张"); break;
                case 4: System.out.println("面值为5的有：" + moneyNum[i] + "张"); break;
                case 5: System.out.println("面值为1的有：" + moneyNum[i] + "张"); break;
            }
        }
    }
}

买卖股票的最好时机(二)

题目链接：牛客网_买卖股票的最好时机(二)

描述：假设数组prices，长度为n，其中prices[i]是某只股票在第i天的价格，请根据这个价格数组，返回买卖股票能获得的最大收益

可以多次买卖该只股票，但是再次购买前必须卖出之前的股票

如果不能获取收益，请返回0

假设买入卖出均无手续费

输入描述：
第一行输入一个正整数 n ，表示数组 prices 的长度
第二行输入 n 个正整数，表示数组中prices的值
输出描述：输出最大收益

示例1
输入
1
2
7
>8 9 2 5 4 7 1
输出：7
说明：
在第1天(股票价格=8)买入，第2天(股票价格=9)卖出，获利9-8=1
在第3天(股票价格=2)买入，第4天(股票价格=5)卖出，获利5-2=3
在第5天(股票价格=4)买入，第6天(股票价格=7)卖出，获利7-4=3
总获利1+3+3=7，返回7

示例2
输入：
1
2
5
>5 4 3 2 1
输出：0
说明：由于每天股票都在跌，因此不进行任何交易最优。最大收益为0。

示例3
输入：
1
2
5
>1 2 3 4 5
输出：4
说明：第一天买进，最后一天卖出最优。中间的当天买进当天卖出不影响最终结果。最大收益为4。

思路：只要当天价格比上一天价格大，就累加，然后算出最大利润即可

public static void main(String[] args) {
    Scanner in = new Scanner(System.in);
    int n = in.nextInt();
    int[] prices = new int[n];
    for (int i = 0; i < prices.length; i++) {
        prices[i] = in.nextInt();
    }
    // 计算
    int sum = 0;
    for (int i = 1; i < n; i++) {
        if(prices[i] > prices[i-1]) { // 如果任何一天比前一天价格高，就在前一天买入今天卖
            sum += (prices[i]-prices[i-1]);
        }  
    }
    System.out.println(sum);
    
    // 或者
    int total = 0;
    for(int i = 0; i < len - 1;i++) {
        if(prices[i] < prices[i+1]) {
            total += prices[i+1] - prices[i];
        }
    }
}

组队竞赛

题目链接：牛客网_组队竞赛

描述：牛牛举办了一次编程比赛，参加比赛的有3*n个选手，每个选手都有一个水平值a_i。现在要将这些选手进行组队，一共组成n个队伍，即每个队伍3人。牛牛发现队伍的水平值等于该队伍队员中第二高水平值。例如:
一个队伍三个队员的水平值分别是3，3，3。那么队伍的水平值是3
一个队伍三个队员的水平值分别是3，2，3。那么队伍的水平值是3
一个队伍三个队员的水平值分别是1，5，2。那么队伍的水平值是2
为了让比赛更有看点，牛牛想安排队伍使所有队伍的水平值总和最大。
如样例所示：如果牛牛把6个队员划分到两个队伍
如果方案为：team1:{1,2,5}, team2:{5,5,8}, 这时候水平值总和为7.
而如果方案为：team1:{2,5,8}, team2:{1,5,5}, 这时候水平值总和为10.
没有比总和为10更大的方案,所以输出10.
输入描述：输入的第一行为一个正整数n(1 ≤ n ≤ 10^5)。第二行包括3*n个整数a_i(1 ≤ a_i ≤ 10^9),表示每个参赛选手的水平值。
输出描述：输出一个整数表示所有队伍的水平值总和最大值

示例1
输入：
1
2
2
5 2 8 5 1 5
输出：10

思路：先排序，比如排完序 1 2 3 4 5 6 7 8 9 这九个数；组队思路是这样的，第一个最后两个（1 8 9），剩下 2 3 4 5 6 7，第一个最后两个（2 6 7），剩下3 4 5一组。就是第一个和最后两个，再把已经组队的删掉，然后再循环，第一个最后两个。那么中位数可以看到是 8 6 4，找到中位数在整个排序后的素组和下标的规则是 data[data.length-(2*(i+1))]，再加在一起。最重要的是 result一定要是long，int会越界。

public static void main(String[] args) {
    Scanner scanner = new Scanner(System.in);
    int n = scanner.nextInt();;
    long[] data = new long[3 * n];
    for (int i = 0; i < data.length ; i++) {
        data[i] = scanner.nextLong();
    }
    Arrays.sort(data); // 从小到大排序
    long result = 0;
    for (int i = 0; i < n; i++) {
        result += data[data.length - (2 * (i + 1))];
    }
    System.out.println(result);
}

public static void main(String[] args) {
    Scanner scan = new Scanner(System.in);
    int n = scan.nextInt();
    ArrayList<Long> arr = new ArrayList<>();
    List<Long> list = new ArrayList<>();
    for (int i = 0; i < 3*n; i++) {
        arr.add(scan.nextLong());
    }
    Collections.sort(arr);
    list = arr.subList(n,3*n);
    long sum = 0;
    for(int i = 0;i < list.size();i++){
        if(i%2 == 0){
            sum += list.get(i);
        }
    }
    System.out.println(sum);
}

区间问题

合并区间

题目链接：LeetCode_56. 合并区间

贪心策略:

先按照区间的「左端点」排序:此时我们会发现，能够合并的区间都是连续的，b.然后从左往后，按照求「并集」的方式，合并区间。

如何求并集: 由于区间已经按照「左端点」排过序了，因此当两个区间「合并」的时候，合并后的区间：

左端点就是「前一个区间」的左端点;
右端点就是两者「右端点的最大值」。

public int[][] merge(int[][] intervals) {
    List<int[]> result = new ArrayList<>();
    Arrays.sort(intervals, (a, b) -> Integer.compare(a[0], b[0]));  // 升序排序
    for(int i = 0; i < intervals.length - 1; i++){
        if(intervals[i][1] >= intervals[i+1][0]){
            intervals[i+1][0] = intervals[i][0];
            intervals[i+1][1] = Math.max(intervals[i][1], intervals[i+1][1]);
        }else{
            result.add(intervals[i]);
        }
    }
    // 最后一个对比完记得加入result数组中
    result.add(intervals[intervals.length - 1]);
    int[][] reIntervals = new int[result.size()][2];
    for(int i = 0; i < result.size(); i++){
        reIntervals[i] = result.get(i);
    }
    return reIntervals;
}

非重叠区间

题目链接：LeetCode_435. 无重叠区间

贪心策略:

按照「左端点」排序;
当两个区间「重叠」的时候，为了能够「在移除某个区间后，保留更多的区间」，我们应该把「区间范围较大」的区间移除。

如何移除区间范围较大的区间：由于已经按照「左端点」排序了，因此两个区间重叠的时候，应该移除「右端点较大」的区间

public int eraseOverlapIntervals(int[][] intervals) {
    Arrays.sort(intervals, (a,b) -> Integer.compare(a[0], b[0])); // 升序排列
    int count = 0; // 统计需要移除的个数
    for(int i = 0; i < intervals.length - 1; i++){
        if(intervals[i][1] > intervals[i + 1][0]) { // 代表存在重复
            count++;
            intervals[i+1][1] = Math.min(intervals[i][1], intervals[i + 1][1]); // 修改下一段区间起点位置
        }
    }
    return count;
}

重叠区间数量

题目链接：LeetCode_452. 用最少数量的箭引爆气球

贪心策略:

按照左端点排序，我们发现，排序后有这样一个性质:「互相重叠的区间都是连续的」;
这样，我们在射箭的时候，要发挥每一支箭「最大的作用」，应该把「互相重叠的区间」统一引爆。

如何求互相重叠区间?

由于我们是按照「左端点」排序的，因此对于两个区间，我们求的是它们的「交集」:

左端点为两个区间左端点的「最大值」(但是左端点不会影响我们的合并结果，所以可以忽略)
右端点为两个区间右端点的「最小值」。

// 可以用 合并区间的代码，只需要改三个字母即可，其中要注意安全比较
public int findMinArrowShots(int[][] points) {
    return merge(points); // 返回列表大小即可
}
public int merge(int[][] intervals) { // 合并区间代码
    int cnt = 0;
    Arrays.sort(intervals, (a, b) -> Integer.compare(a[0], b[0])); // 安全比较
    List<int[]> merged = new ArrayList<>();
    for(int i = 0; i < intervals.length; i++){
        int L = intervals[i][0],R = intervals[i][1];
        if(merged.size() == 0 || merged.get(merged.size() - 1)[1] < L){
            merged.add(new int[]{L,R});
        } else { // 注意就是这里，把max换成min即可
            merged.get(merged.size() - 1)[1] = Math.min(merged.get(merged.size() -1)[1],R);    
        }
    }
    return merged.size();
}

区间套娃

题目链接：Leetcode_354. 俄罗斯套娃信封问题

思路：重写排序 + 贪心 + 二分

当我们把整个信封按照「下面的规则」排序之后:

左端点不同的时候:按照「左端点从小到大」排序;
左端点相同的时候:按照「右端点从大到小」排序

此时问题就变成了仅考虑信封的「右端点」，完全变成「最长上升子序列」模型。就可以用「贪心+二分」优化算法。

// 先按长排序, 然后按照O(N^2)的最长递增子序列的思想来做
public int maxEnvelopes(int[][] envelopes) {
    int n = envelopes.length;
    if(n < 1) return 0;
    int max = 1;
    int[] dp = new int[n];
    Arrays.fill(dp, 1);
    Arrays.sort(envelopes, (a,b) -> (a[0]-b[0]));
    for(int i = 1; i < n; ++i) {
        for(int j = 0; j < i; ++j) {
            if(envelopes[i][0] > envelopes[j][0] && envelopes[i][1] > envelopes[j][1])
                dp[i] = Math.max(dp[i], dp[j] + 1);
        }
        max = Math.max(max, dp[i]);
    }
    return max;
}
// O(NlogN)的做法, 按照长度升序, 同长则宽度降序排列, 然后使用O(logN)的最长递增子序列解法(链接在评论中)来做即可. 排序后等于把在二维(长、宽)上的最长递增子序列问题转换成一维(宽)上的最长递增子序列的查找, 因为对于长度来说已经满足递增, 只需要在宽度上也递增即为递增序列, 同长时按宽度降序排列的原因是避免同长时宽度小的也被列入递增序列中, 例如[3,3], [3,4],如果宽度也按升序来排列, [3,3]和[3,4]会形成递增序列, 而实际上不行.
public int maxEnvelopes(int[][] envelopes) {
    int maxL = 0;
    int[] dp = new int[envelopes.length];
    Arrays.sort(envelopes, (a, b) -> (a[0] == b[0] ? b[1] - a[1] : a[0] - b[0]));
    for(int[] env : envelopes) {
        int lo = 0, hi = maxL;
        while(lo < hi) {
            int mid = lo + (hi - lo) / 2;
            if(dp[mid] < env[1]) lo = mid + 1;
            else hi = mid;
        }
        dp[lo] = env[1];
        if(lo == maxL) maxL++;
    }
    return maxL;
}

整数问题

坏了的计算器

题目链接：LeetCode_991. 坏了的计算器

贪心策略：【正难则反】

当「反着」来思考的时候，我们发现

当 end<= begin 的时候，只能执行「加法」操作;
当 end > begin 的时候，对于「奇数」来说，只能执行「加法」操作;对于「偶数」来说，最好的方式就是执行「除法」操作

这样的话，每次的操作都是「固定唯一」的。

public int brokenCalc(int startValue, int target) {
    if(startValue >= target) {
        return startValue - target;
    }
    if(target % 2 == 0) {
        return 1 + brokenCalc(startValue, target / 2);
    } else {
        return 1 + brokenCalc(startValue, target + 1);
    }
}

整数替换

题目链接：LeetCode_397. 整数替换

贪心策略: 我们的任何选择，应该让这个数尽可能快的变成1

对于偶数：只能执行除 2操作，没有什么分析的;

对于奇数：

当 n == 1 的时候，不用执行任何操作;
当 n == 3 的时候，变成 1 的最优操作数是 2;
当 n > 1 && n%4 == 1 的时候，那么它的二进制表示是……01，最优的方式应该选择 -1，这样就可以把末尾的1干掉，接下来执行除法操作，能够更快的变成
当 n > 3 && n%4 == 3 的时候，那么它的二进制表示是……11，此时最优的策略应该是 +1，这样可以把一堆连续的1转换成 0，更快的变成 1。

public int integerReplacement(int n) {
  return (int)func((long)n);
}
public long func(long n){
    if(n == 1) return 0;
    if( n % 2 == 0){
        return  1 + func(n / 2);
    } else  { 
      return 1 + Math.min(func(n + 1), func(n - 1));
    }
}

可被三整除的最大和

题目链接：LeetCode_1262. 可被三整除的最大和

思路：正难则反 + 贪心 + 分类讨论

正难则反：可以先把所有的数累加在一起，然后根据累加和的结果，贪心的删除一些数。

分类讨论：设累加和为 sum，用 x 标记 %3 == 1 的数，用 y 标记 %3 == 2 的数。那么根据 sum 的余数，可以分为下面三种情况:

sum %3 == 0，此时所有元素的和就是满足要求的，那么我们一个也不用删除;，
sum %3 == 1，此时数组中要么存在一个 x，要么存在两个 y。因为我们要的是最大值，所以应该选择 x 中最小的那么数，记为x1，或者是y 中最小以及次小的两个数，记为 y1，y2。

那么，我们应该选择两种情况下的最大值：max(sum-x1，sum - y1 -y2）；
sum %3 == 2，此时数组中要么存在一个 y，要么存在两个 x。因为我们要的是最大值，所以应该选择 y 中最小的那么数，记为y1，或者是x 中最小以及次小的两个数，记为 x1，x2。

那么，我们应该选择两种情况下的最大值：max(sum-y1，sum - x1 -x2）；

public int maxSumDivThree(int[] nums) {
    int n = nums.length;
    int[][] dp = new int[n][3]; // dp[i][j]表示前i个数，模3=j时的最大值
    dp[0][nums[0] % 3] = nums[0];
    for (int i = 1; i < n; i++) {
        for (int j = 0; j < 3; j++) {
            //先将上一个状态转移过来
            dp[i][j] = Math.max(dp[i][j], dp[i - 1][j]);
            //转移每个模3=j的数
            int sum = dp[i - 1][j] + nums[i];
            dp[i][sum % 3] = Math.max(dp[i][sum % 3],sum);
        }
    }
    return dp[n - 1][0];
}

单调递增的数字

题目链接：LeetCode_738. 单调递增的数字

解法(贪心)

为了方便处理数中的每一位数字，可以先讲整数转换成字符串
从左往右扫描，找到第一个递减的位置
从这个位置向前推，推到相同区域的最左端
该点的值 -1，后面的所有数统一变成 9

思路：从右向左扫描数字，若发现当前数字比其左边一位（较高位）小，则把其左边一位数字减1，并将该位及其右边的所有位改成9

public static int monotoneIncreasingDigits(int n) {
    String s = String.valueOf(n);
    int length = s.length();
    char[] chars = s.toCharArray();
    int flag = length;
    for (int i = length - 1; i >= 1; i--) {
        if (chars[i] < chars[i - 1]) {
            flag = i;
            chars[i - 1]--;
        }
    }
    for (int i = flag; i < length; i++) {
        chars[i] = '9';
    }
    return Integer.parseInt(new String(chars));
}

排列问题

排列数字使相邻数字不等

题目链接：LeetCode_1054. 距离相等的条形码

贪心策略:

每次处理一批相同的数字，往n个空里面摆放;
每次摆放的时候，隔一个格子摆放一个数;
优先处理出现次数最多的那个数

public int[] rearrangeBarcodes(int[] barcodes) {
    int n = barcodes.length,temp;
    // 从左边开始找到相邻条形码相同，将后一个条形码与后面不同的条形码交换
    for(int i = 1; i < n; i++){
        if(barcodes[i] == barcodes[i-1]){
            for(int j = i; j < n;j++){
                if(barcodes[j] != barcodes[i]){
                    swap(barcodes,i,j);
                    break;
                }
            }
        }
    }
    // 从右边再来一次
    for(int i = n - 2;i >= 0;i--){
        if(barcodes[i] == barcodes[i + 1]){
            for(int j = i; j >= 0; j--){
                if(barcodes[j] != barcodes[i]){
                    swap(barcodes,i,j);
                    break;
                }
            }
        }
    }
    // 从左边不能保证[2,1,1]、[2,3,1,1,1]，从右边不能保证[1,1,2]等，但左右都来一次就能保证结果满足      
    return barcodes;
}
public void swap(int[] barcodes, int i, int j){
    int temp = barcodes[i];
    barcodes[i] = barcodes[j];
    barcodes[j] = temp;
}

排列字符串使相邻字符不等

题目链接：LeetCode_767. 重构字符串

Java大根堆，每次取出现频率最多的2个字符组合，重点对于剩1个元素时情况的讨论

public String reorganizeString(String s) {
    int n = s.length();
    int[] cnt = new int[26];
    for (int i = 0; i < n; i++) {
        char c = s.charAt(i);
        cnt[c-'a']++;
    }
    PriorityQueue<int[]> pq = new PriorityQueue<>((o1,o2) -> (o2[1]-o1[1]));
    for (int i = 0; i < 26; i++) {
        if (cnt[i] != 0) pq.add(new int[] {i,cnt[i]});
    }
    assert !pq.isEmpty();
    if (pq.peek()[1] > n/2 + 1) return "";
    StringBuilder sb = new StringBuilder();
    while (pq.size() > 1) {
        int[] a = pq.poll(), b = pq.poll();
        assert b != null;
        sb.append((char) ('a'+a[0]));
        sb.append((char) ('a'+b[0]));
        if (--a[1] > 0) pq.add(a);
        if (--b[1] > 0) pq.add(b);
    }
    if (pq.isEmpty()) return sb.toString();
    if (pq.peek()[1] > 1) return "";
    return sb.append((char) ('a'+pq.peek()[0])).toString();
}

行驶问题

加油站

题目链接：LeetCode_134. 加油站

暴力解法:

依次枚举所有的起点:
从起点开始，模拟一遍加油的流程

贪心优化:

当从 i位置出发，走了 step 步之后，如果失败了。那么[i，i+ step]这个区间内任意一个位置作为起点，都不可能环绕一圈。
因此我们枚举的下一个起点，应该是 i + step + 1

public int canCompleteCircuit(int[] gas, int[] cost) {
   int balance = 0; // 只要sumOfCost <= sumOfGas 就代表者一定是可以到达的
   int minIndex = 0, minBalance = 0; // 具体从哪里出发的话就是从欠债最多的那个加油站就可以的
   for (int i = 0; i < gas.length; i++) {
       balance += gas[i] - cost[i];
       if (balance < minBalance) {
           minBalance = balance;
           minIndex = i + 1; // 这里是问的第几个加油站
       }
   }
   return balance >= 0 ? minIndex : -1;
}

序列问题

递增的三元子序列

题目链接：LeetCode_334. 递增的三元子序列

贪心策略:

最长递增子序列的简化版。
不用一个数组存数据，仅需两个变量即可。也不用二分插入位置，仅需两次比较就可以找到插入位置

public boolean increasingTriplet(int[] nums) {
    int a = 2147483647, b = a;
    for (int n: nums) 
        if (n <= a) a = n;
        else if (n <= b) b = n;
        else return true;
    return false;
}

最长递增子序列

题目链接：LeetCode_300. 最长递增子序列

贪心策略:

在考虑最长递增子序列的长度的时候，其实并不关心这个序列长什么样子，我们只是关心最后一个元素是谁。
这样新来一个元素之后，我们就可以判断是否可以拼接到它的后面。
因此，我们可以创建一个数组，统计长度为 x的递增子序列中，最后一个元素是谁。
为了尽可能的让这个序列更长，我们仅需统计长度为 x的所有递增序列中最后一个元素的「最小值」。
统计的过程中发现，数组中的数呈现「递增」趋势，因此可以使用「二分」来查找插入位置。

思路：

dp[i]: 所有长度为i+1的递增子序列中, 最小的那个序列尾数。由定义知dp数组必然是一个递增数组, 可以用 maxL 来表示最长递增子序列的长度。对数组进行迭代, 依次判断每个数num将其插入dp数组相应的位置:

num > dp[maxL], 表示num比所有已知递增序列的尾数都大, 将num添加入dp数组尾部, 并将最长递增序列长度maxL加1
dp[i - 1] < num <= dp[i], 只更新相应的dp[i]

class Solution {
    public int lengthOfLIS(int[] nums) {
        int maxL = 0;
        int[] dp = new int[nums.length];
        for(int num : nums) {  // 二分法查找, 也可以调用库函数如binary_search
            int lo = 0, hi = maxL;
            while(lo < hi) {
                int mid = lo + (hi - lo) / 2;
                if(dp[mid] < num) {
                    lo = mid + 1;
                } else {
                    hi = mid;
                }
            }
            dp[lo] = num;
            if(lo == maxL) {
                maxL++;
            } 
        }
        return maxL;
    }
}

贪心算法详解

基本定义

核心性质

贪心算法与动态规划的差异

算法框架

典型应用场景

图论问题

组合优化问题

经典例题详解

变种与挑战问题

贪心策略的代码实现范式

关键数据结构

经典问题实现

区间调度（最大不重叠区间）

哈夫曼编码（数据压缩）

正确性证明与复杂度分析

证明方法

复杂度分析

适用条件判断

算法题

分发糖果

盛最多水的容器

背包问题

购物清单（带条件的背包问题）

活动时间安排问题

最小生成树（克鲁斯卡尔算法）

线段覆盖（Lines cover）

数字组合问题

拼数

找零钱问题

买卖股票的最好时机(二)

组队竞赛

区间问题

合并区间

非重叠区间

重叠区间数量

区间套娃

整数问题

坏了的计算器

整数替换

可被三整除的最大和

单调递增的数字

排列问题

排列数字使相邻数字不等

排列字符串使相邻字符不等

行驶问题

加油站

序列问题

递增的三元子序列

最长递增子序列